INTERFÉRENCES LUMINEUSES

INTERFÉRENCES LUMINEUSES

Lorsqu’on éclaire un plan matériel par deux sources ponctuelles, le phénomène observé ne résulte pas toujours de la superposition des intensités lumineuses émises par les deux sources. Si elles émettent des vibrations parallèles et monochromatiques, on peut avoir théoriquement deux sortes de phénomènes suivant que les vibrations ont des fréquences différentes ou la même fréquence. Dans le premier cas se produisent des battements optiques, qui peuvent être détectés si les fréquences sont peu différentes, et que l’on perçoit alors dans le domaine des ondes radio. Dans le second cas, les deux sources monochromatiques qui émettent des vibrations parallèles de même fréquence donnent lieu à des phénomènes d’interférences; dans certaines régions du plan d’observation, les vibrations sont en phase et les amplitudes s’ajoutent: il y a maximum de lumière; dans d’autres régions, les vibrations sont en opposition de phase et les amplitudes se retranchent: il y a minimum de lumière.

Il est impossible d’observer des interférences avec deux sources lumineuses ordinaires distinctes. Deux lasers différents peuvent interférer en principe, mais les expériences sont très difficiles à réaliser. On utilise pratiquement dans tous les cas une source unique et un système interférentiel qui divise l’onde incidente en deux ou plusieurs ondes; après avoir parcouru des chemins différents, ces ondes se superposent en donnant des interférences.

1. Principe des interférences

Vibrations lumineuses

Augustin Fresnel a été le premier à expliquer les phénomènes de l’optique physique en admettant que la lumière est constituée par des vibrations transversales; il assimilait les vibrations lumineuses aux vibrations élastiques transversales des solides. Cette dernière hypothèse aboutit à de nombreuses contradictions qui ont conduit à remplacer la théorie mécanique de Fresnel par la théorie électromagnétique de Maxwell. Dans celle-ci la lumière apparaît comme due à la propagation simultanée d’un champ électrique et d’un champ magnétique, les vibrations du champ électrique représentant la vibration lumineuse dans l’espace où se propage la lumière.

Une vibration lumineuse en un point de l’espace est représentée par un vecteur ayant ce point pour origine: l’extrémité de ce vecteur décrit une certaine courbe dans un plan perpendiculaire à la direction de propagation, et sa projection sur un axe de ce plan est une fonction périodique du temps. La fonction périodique la plus simple est la fonction sinusoïdale, et l’on représentera la vibration lumineuse par une fonction sinusoïdale du temps. Elle pourra s’écrire, à l’origine du temps:

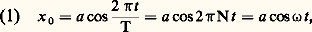où a est l’amplitude de la vibration, 諸 = 2 神 N = 2 神/T la pulsation , N la fréquence et T la période . Au point M d’abscisse z , la vibration est à l’instant t ce qu’elle était au point O au temps t 漣 (z /V), si V est la vitesse de propagation (fig. 1). On aura donc:

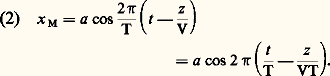VT =ⁿ est la longueur d’onde de la vibration. En posant 﨏 = 2 神 z /ⁿ , on peut écrire:

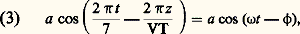﨏 étant la différence de phase entre la vibration en M et la vibration en O.

La longueur d’ondeⁿ est caractéristique d’une radiation donnée dans un milieu déterminé. Si une même radiation change de milieu, sa fréquence reste fixe, mais sa longueur d’onde varie. On caractérise souvent les radiations par leur longueur d’onde dans le vide^c = c/N avec c = 3 . 10⁸ m/s. Dans un milieu d’indice de réfraction n où se propage la vibration de fréquence N, sa longueur d’onde seraⁿ = V/N =^c V/c =^c /n . L’indice n étant toujours plus grand que 1, les longueurs d’onde sont plus courtes dans les milieux matériels que dans le vide.

La relation précédente s’écrit:

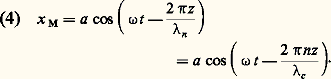Le produit 嗀 = nz est le chemin optique entre O et M ou encore la différence de marche entre ces deux points. Les différences de phase 﨏 sont reliées aux différences de marche 嗀 par l’expression:

On utilisera par la suite la notation, longueur d’onde dans l’air, qui diffère très peu de^c .

Production des interférences

Lorsque deux ou plusieurs ondes lumineuses se superposent, on ne peut pas, en général, décrire d’une manière simple les phénomènes observés. Pour préciser les conditions auxquelles deux faisceaux lumineux doivent satisfaire pour pouvoir interférer, il faudrait connaître le mécanisme de l’émission par une source lumineuse. Ce mécanisme n’est pas encore complètement élucidé, mais il semble pouvoir être admis, pour les problèmes que l’on aura à traiter, que les ondes électromagnétiques ne sont pas émises de façon continue, mais «par paquets», c’est-à-dire par trains d’ondes provenant des divers atomes. Les atomes n’émettent que pendant un temps limité 精; si l’on attend un temps important par rapport à 精, les vibrations observées à l’instant initial auront disparu, d’autres auront pris le relais, mais elles n’auront plus aucune relation avec les vibrations initiales. La vibration d’un atome peut être représentée par l’expression:

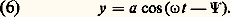Au bout d’un temps supérieur à 精, la vibration précédente cesse, soit par amortissement, soit parce qu’il y a eu choc avec d’autres atomes. Lorsque l’atome réémet une vibration, l’amplitude a et la phase 切 ont complètement changé. Le phénomène se reproduit ainsi un très grand nombre de fois par seconde.

Considérons un point qui reçoit deux vibrations d’amplitude a et b provenant de deux atomes. À l’instant où la différence de phase est 淋, le carré de l’amplitude résultante A est:

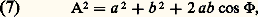mais, pendant l’observation, A varie un très grand nombre de fois par suite des variations de a , b , et 淋. L’intensité perçue est la valeur moyenne du carré A² de l’amplitude prise sur un intervalle de temps pendant lequel la différence de phase 淋 varie un très grand nombre de fois et prend toutes les valeurs possibles. Le terme en cos 淋 prend donc autant de fois des valeurs positives que des valeurs négatives et s’élimine en moyenne. Des atomes différents émettent des vibrations qui ne peuvent interférer et que l’on appellera des vibrations incohérentes . Il ne pourrait y avoir cohérence que si les phénomènes étaient observés dans un temps nettement inférieur à 精. Cela est pratiquement impossible avec les sources ordinaires pour lesquelles le temps 精 est toujours très petit, mais peut être réalisé avec les lasers. On peut rapprocher ce dernier cas des phénomènes acoustiques produits par deux diapasons différents qui peuvent donner des interférences simplement parce qu’on a le temps de les observer avant qu’il soit nécessaire de relancer l’un d’eux.

Dans le cas des sources thermiques , les interférences résultant de la composition de deux ou plusieurs vibrations ne peuvent se produire que dans des conditions déterminées: les vibrations doivent provenir d’une même source (sauf pour les lasers) et être parallèles. Un appareil interférentiel a donc pour rôle essentiel de diviser l’onde incidente en deux ou plusieurs ondes qui, après avoir parcouru des chemins différents, se superposent en donnant lieu à des phénomènes d’interférences. Il existe beaucoup de types différents de diviseurs d’ondes. En particulier, les lames biréfringentes dédoublent un rayon incident en deux rayons, l’un ordinaire, l’autre extraordinaire, qui accomplissent des chemins optiques différents puisque l’indice de la lame n’est pas le même pour les deux rayons. Dans la région où ils se superposent, ils peuvent interférer à condition que les vibrations soient cohérentes, ce qui s’obtient à l’aide d’un polariseur placé avant la lame, et qu’elles soient parallèles, ce qui est possible en plaçant un analyseur après la lame. En sélectionnant le type de cristal employé et la façon dont il est taillé, on observera de très belles figures d’interférences.

2. Interférences à deux ondes

Franges de Young

Considérons deux trous très petits A¹ et A² (fig. 2 a) identiques, percés dans un écran opaque et équidistants de la source lumineuse S. D’après les lois de l’optique géométrique, on devrait voir seulement deux taches lumineuses en A ¹ et A ². En fait, chaque petite ouverture diffracte la lumière qui s’étale dans le plan P. Tout se passe comme si A¹ et A² étaient de véritables sources, mais les vibrations qu’elles diffractent sont dues à une source unique S et sont par conséquent cohérentes. C’est dans la région M¹M² où se superposent les faisceaux diffractés que l’on peut observer les franges d’interférences. En un point quelconque M de l’écran P la différence de marche 嗀 est (fig. 2 b):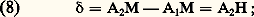

en considérant les triangles A¹A²H et COM, et en posant CO = D, OM = y , A¹A² = 2 a , on a:

Comme les ouvertures A¹ et A² sont identiques, elles diffractent le même flux, et dans l’expression (7) les amplitudes a et b sont pratiquement égales. La variation de l’intensité lumineuse dans le plan P est donnée par: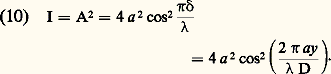

En première approximation, les franges sont des droites parallèles et équidistantes. Elles sont dirigées perpendiculairement au plan de la figure 2 b. La formule (10) montre que les maximums de lumière, c’est-à-dire les franges brillantes, sont donnés par:

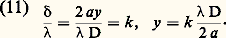Le rapport k = 嗀/ est appelé ordre d’interférence . Pour les franges sombres:

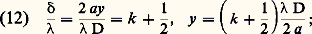on a une frange brillante en O puisque y = 嗀 = 0.

Phénomènes en lumière blanche

Considérons une source ponctuelle de lumière blanche. À chaque radiation monochromatique correspond un système de franges, et tous ces systèmes s’ajoutent en intensité dans le plan d’observation.

Supposons que toutes les radiations aient même énergie et traçons sur un graphique les variations de I en fonction du nombre d’ondes 靖 = 1/ que l’on mesure en cm^-1. Pour tracer convenablement le graphique, il faudrait tenir compte de la sensibilité spectrale de l’œil; on supposera simplement que la partie utile est comprise entre 靖 = 13 000 cm^-1 ( = 0,8 猪m, rouge) et 靖 = 25 000 cm^-1 ( = 0,4 猪m, bleu). Pour chaque radiation l’intensité est donnée, à un facteur constant près, par la relation (10).

Au point O (fig. 2 b) sur la frange centrale, 嗀 = 0 pour toutes les radiations et la courbe I = f ( 靖) est une droite parallèle à l’axe des abscisses (fig. 3); en O la frange centrale est blanche. À faible distance du centre O ( 嗀 = 﨎), la courbe de l’intensité est une sinusoïde très allongée; l’intensité est plus faible pour les courtes longueurs d’onde que pour les grandes longueurs d’onde; le violet est plus atténué que le rouge, et la teinte résultante est rougeâtre. Plaçons-nous en un point du plan P tel que 嗀 = 0,28 猪m. D’après (10), I = 0 si 嗀 =/2, c’està-dire si = 2 嗀 = 0,56 猪m; la sinusoïde est tangente à l’axe des abscisses au point 靖 = 18 000 cm^-1 ( = 0,565 猪m) correspondant au jaune vert; au point considéré, on aurait la première frange noire si la source émettait seulement la radiation = 0,565 猪m. La courbe montre que l’intensité reste partout faible, sauf aux extrémités du spectre visible, auxquelles l’œil est très peu sensible. Dans la région considérée du plan P, le champ est un peu lumineux et il présente une teinte pourpre, mélange de rouge et de violet.

Écartons-nous très peu de cette position en nous rapprochant de O. La différence de marche devient 嗀 = 0,28 猪m 漣 﨎. La couleur est plus riche en rouge et moins riche en violet, la teinte pourpre vire au rouge. En un point plus éloigné de la frange centrale 嗀 = 0,28 猪m + 﨎, la teinte est plus bleue (indigo). Un léger changement de 嗀 fait virer rapidement la teinte pourpre, et l’œil est très sensible à ce changement de teinte. La teinte correspondant à 嗀 = 0,28 猪m est appelée teinte sensible du premier ordre.

Pour 嗀 = 0,4 猪m (fig. 4), la courbe présente un minimum dans le rouge ( 靖 = 13 000 cm^-1, = 0,8 猪m) et un maximum dans le violet ( 靖 = 25 000 cm^-1, = 0,4 猪m). La teinte résultante est bleue. On peut ainsi observer toute une série de teintes qui présentent des colorations très vives si l’on ne s’écarte pas trop loin de la frange centrale. À chaque valeur de 嗀 correspond une teinte déterminée. Ces teintes sont données dans une table dite échelle des teintes de Newton. La frange centrale est blanche: on a l’échelle des teintes à centre blanc. Dans d’autres expériences, la frange centrale est noire et l’on obtient une autre échelle des teintes de Newton dite échelle à centre noir.

Pour des valeurs croissantes de 嗀, la sinusoïde de la figure 3 se resserre de plus en plus, on a une série de maximums et de minimums. Les colorations cessent d’être visibles dès que 嗀 dépasse 3 ou 4 猪m: l’œil perçoit une impression de blanc, appelé blanc d’ordre supérieur . Par ailleurs, lorsque 嗀 augmente, des radiations de plus en plus nombreuses s’éteignent dans le spectre: si on reçoit du blanc d’ordre supérieur dans un spectroscope, le spectre apparaît sillonné de cannelures noires (spectre cannelé ).

Franges d’égale inclinaison par réflexion sur une lame à faces parallèles

Considérons une lame à faces parallèles d’épaisseur e et d’indice n (fig. 5 a), éclairée par une source étendue S de lumière monochromatique. Un rayon incident S¹I¹ se dédouble en I¹ sur la première face de la lame et donne naissance à un rayon transmis I¹J¹ et à un rayon réfléchi I¹L¹. Le rayon I¹J¹ se réfléchit en J¹ sur la seconde face de la lame et sort suivant K¹L¹ parallèlement à I¹L¹. Les deux rayons parallèles I¹L¹ et K¹L ¹ se rencontrent en F dans le plan focal de l’objectif O et ils interfèrent. Soit S² un autre point de la source S; parmi les rayons émis par S², considérons le rayon S²I² parallèle au rayon S¹L¹. Le même phénomène se reproduit, et les deux rayons J²L² et K²L ² aboutissent au même point F où ils interfèrent. Il est facile de voir que les différences de marche

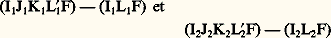sont égales. Les phénomènes d’interférence produits en F par S¹ et S² sont incohérents, mais, comme ils sont identiques, la visibilité du phénomène reste la même. Cela est vrai pour tous les rayons émis par les différents points de la source S qui sont parallèles à S¹I¹: ils donnent le même phénomène au point F. Les rayons incidents parallèles correspondant à une autre inclinaison aboutissent en un autre point du plan focal.

Les phénomènes d’interférences produits par une lame à faces parallèles observés dans le plan focal d’un objectif sont nets quelle que soit l’étendue de la source. Dans ce qui précède, on a négligé les rayons plusieurs fois réfléchis car, par suite de la décroissance rapide de leurs amplitudes, ils ne produisent que des perturbations négligeables. En effet, si l’on prend l’amplitude incidente égale à l’unité, les formules de Fresnel donnent alors, pour les amplitudes des rayons réfléchis et transmis successifs, les valeurs portées sur la fig. 5 b. Les amplitudes sont pratiquement négligeables à partir du troisième rayon, et il suffit de faire intervenir les rayons (1) et (2). Par ailleurs, on étudiera les phénomènes sous une incidence voisine de l’incidence normale. Calculons la différence de marche en F. Soit un rayon incident SI faisant avec la normale l’angle d’incidence i (fig. 5 c). Après réflexion sur les deux faces de la lame, on a les deux rayons IL et KL . Ces deux rayons provenant du même rayon incident SI, leur différence de phase reste constante à partir de K et H, H étant le pied de la perpendiculaire abaissée de K sur IL. Entre I et KH, le rayon IL accomplit le trajet IH dans l’air et le rayon KL le trajet IJK dans le milieu d’indice n . La différence de marche est donc 嗀 = 2n IJ 漣 IH. Mais le rayon IL se réfléchit de l’air sur le verre, c’est-à-dire d’un milieu moins réfringent sur un milieu plus réfringent, tandis que le rayon JKL se réfléchit du verre sur l’air, soit d’un milieu plus réfringent sur un milieu moins réfringent. On montre qu’il faut alors ajouter un retard supplémentaire égal à/2 et la différence de marche s’écrit:

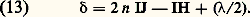L’étude géométrique de la figure 5 c conduit au résultat suivant:

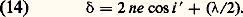嗀 = C ^te si i = C ^te : les franges sont des anneaux ayant pour axe la normale à la lame. L’observation peut se faire suivant le schéma de la figure 6. La source S est une source étendue de lumière monochromatique envoyant des rayons diversement inclinés sur la lame l après réflexion sur la lame semi-transparente G inclinée à 45⁰. En faisant coïncider la normale à l avec l’axe optique de l’objectif O, on observe dans le plan focal 神 des anneaux de centre F. Tous les points d’un anneau correspondent à une même valeur de l’inclinaison des rayons incidents sur la normale. On appelle ces anneaux des franges d’égale inclinaison.

Les rayons correspondant au même angle d’incidence i sur la lame coupent le plan focal suivant une circonférence de rayon FM. Pour tous les points de cette circonférence, l’ordre d’interférence est constant et égal à:

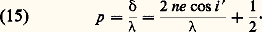Si p = k entier, on aura un anneau brillant et pour p = k + (1/2) un anneau noir. Au centre F, l’ordre d’interférence est:

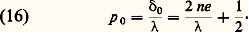Si l’on s’éloigne de ce point, l’ordre d’interférence diminue et, au point M, il est:

K (entier ou fractionnaire) représentant le nombre de franges que l’on voit entre F et

M. En supposant les angles petits: cos i 力 1 漣 (i ²/2), i 力 ni , les formules (15), (16) et (17), donnent: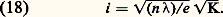

Si l’on a une frange noire en F, cette formule donnera le rayon du K-ième anneau noir. Les rayons des anneaux correspondant au même état d’interférence que le centre varient comme les racines carrées des nombres entiers. Ils se resserrent à mesure que l’on s’écarte du centre F.

Franges d’égale épaisseur en faisceau parallèle, par réflexion

Cas général

Soit maintenant une lame d’épaisseur variable. Supposons que les variations d’épaisseur de la lame soient faibles et l’incidence voisine de l’incidence normale. La lame est éclairée en faisceau parallèle par une source ponctuelle à l’infini (fig. 7). Considérons deux rayons incidents parallèles (1) et (2). Le rayon (1) suit le trajet SIJKL¹, le rayon (2) le trajet SKL². Puisqu’on opère en incidence presque normale, les points I et K sont très rapprochés et l’on peut donc considérer que la lame a une épaisseur e bien définie dans la région IJK. L’objectif O donne en K une image de la lame. Il peut s’agir simplement de l’œil de l’observateur qui accommode sur la lame, le cristallin constituant l’objectif O et la rétine étant alors en K .

Entre K et K , les chemins optiques des deux rayons sont égaux. Il suffit de considérer la différence de marche entre K et la source S. Il est facile de voir que la différence de marche, géométriquement, est 2 ne en incidence presque normale; comme précédemment, il faut ajouter un retard supplémentaire égal à/2. La différence de marche en K (ou en K ) entre les rayons (1) et (2) devient:

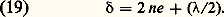Les rayons qui interfèrent ont pratiquement la même amplitude a et l’intensité lumineuse au point K vaut:

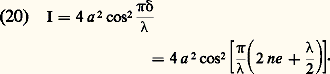Pour un autre point K sur la lame, l’épaisseur e n’est plus la même et l’intensité varie. L’indice de réfraction n étant supposé constant, la différence de marche 嗀 est fonction seulement de l’épaisseur e . En regardant la lame, on voit des franges qui en dessinent les lignes d’égale épaisseur (franges de Fizeau). Les franges brillantes sont données par:

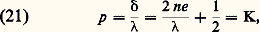et les franges noires par:

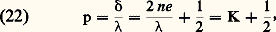Les franges noires correspondent aux épaisseurs e = K/2 n et, lorsqu’on passe d’une frange à la suivante, l’épaisseur de la lame varie de/2n . Par exemple, avec une lame d’air comprise entre deux lames de verre, et pour = 0,6 猪m, on a/2 n = 0,3 猪m.

On peut aussi observer les phénomènes par transmission, mais ils sont peu visibles et moins intéressants.

Coins d’air

On utilise une lame mince d’air comprise entre deux lames de verre formant un petit angle 﨎 (fig. 8). Les franges sont localisées sur la lame et dessinent les lignes d’égale épaisseur: ce sont des droites parallèles à l’arête du coin. Quand on passe d’une frange à la suivante (deux franges de même type), l’épaisseur varie de/2.

Anneaux de Newton

Posons une surface sphérique S (lentille plan-convexe de grand rayon) sur une surface de verre plane P (fig. 9). Observons par réflexion les interférences produites par la lame d’air mince située entre les deux surfaces. Les franges qui dessinent les lignes d’égale épaisseur sont ici des cercles centrés sur le point de contact de la lentille et de la surface de verre: ce sont les anneaux de Newton.

Si R est le rayon de courbure de la surface sphérique S, et K un nombre entier quelconque, le rayon du K-ième anneau noir est donné par:

Interféromètre de Michelson

L’interféromètre de Michelson (fig. 10) comporte essentiellement deux miroirs orthogonaux (M¹ et M²) et une lame de verre (G¹), inclinée à 45⁰ par rapport aux normales aux deux miroirs. La première face de la lame G¹, appelée séparatrice , est semi-réfléchissante: elle réfléchit autant de lumière qu’elle en transmet.

Prenons une source ponctuelle S au foyer d’un objectif ¹; l’interféromètre est éclairé par un faisceau de rayons parallèles. L’un de ces rayons, SA, se dédouble lorsqu’il arrive en A sur la face semi-réfléchissante de la séparatrice G¹. Le rayon réfléchi sur G¹ frappe le miroir M¹ en B¹, revient sur lui-même, traverse G¹ sans déviation et pénètre dans l’objectif ². L’autre rayon traverse G¹, se réfléchit en B² sur le miroir M², revient en arrière, se réfléchit sur la face semi-réfléchissante A de G¹ et se superpose au premier rayon pour traverser l’objectif ². Le premier rayon ne traverse qu’une fois la séparatrice G¹ alors que le deuxième la traverse trois fois. Pour rendre les trajets parcourus aussi identiques que possible, on interpose une lame G², dite compensatrice , sur le premier rayon. Cette lame doit avoir la même épaisseur et être faite du même verre que la lame G¹. Comme une égalité rigoureuse des épaisseurs de G¹ et G² est très difficile à réaliser, on peut compenser la très faible différence éventuelle en inclinant légèrement la compensatrice G².

Par réflexion sur la face semi-réfléchissante A de la séparatrice G¹, le miroir M² a une image en M’². Tout se passe comme s’il y avait des interférences produites par une lame d’air comprise entre M¹ et M ². Si l’image M ² n’est pas parallèle à M¹, il s’agit d’un coin d’air. Si les différentes pièces optiques constituant l’appareil sont parfaites, les franges sont alors rectilignes, parallèles et équidistantes. Pour les voir, on place la pupille de l’œil au foyer F de l’objectif ².

Si l’image M ² est rigoureusement parallèle à M¹, on peut observer les anneaux à l’infini de la lame d’air ainsi formée. On examine alors au moyen d’une loupe le plan focal F où ils sont localisés. L’ensemble de l’objectif ² et de la loupe constitue une lunette visant à l’infini, dont le grossissement sera choisi en fonction du diamètre angulaire des anneaux observés. Il faut remplacer la source ponctuelle S par une source étendue. On peut d’ailleurs supprimer le collimateur et le remplacer par une grande surface diffusante éclairée par une source monochromatique. En déplaçant l’un des miroirs parallèlement à lui-même, on fait varier à volonté le diamètre des anneaux. Si les deux lames G¹ et G² sont bien parallèles, on constate que les anneaux à l’infini sont parfaitement circulaires. Ils se déforment lorsqu’on incline G² par rapport à G¹: d’abord elliptiques, ils deviennent hyperboliques si l’on augmente encore l’inclinaison.

Interféromètre de Mach-Zehnder

Comme l’interféromètre de Michelson, l’interféromètre de Mach-Zehnder est un interféromètre à deux ondes (fig. 11). La lame S¹ sépare le faisceau initial en deux. Après réflexion sur les miroirs M¹ et M², les faisceaux lumineux sont réunis grâce à la lame semi-réfléchissante S².

Quand les miroirs M¹ et M² ne sont pas rigoureusement parallèles, les deux faisceaux forment un petit angle et il apparaît un système de franges d’interférences rectilignes. Un réglage convenable permet de localiser ces franges entre M¹ et S². L’interposition, en cet endroit, d’un objet déphasant qui ne modifie que l’un des faisceaux déforme le système de franges. La disposition des miroirs permet de séparer largement les faisceaux lumineux et d’étudier des objets volumineux au prix de difficultés accrues pour les réglages initiaux et le maintien de la stabilité mécanique et thermique de l’ensemble.

Cet interféromètre est d’utilisation courante pour la mesure des variations de pression dans l’air s’écoulant autour d’une maquette. Ces variations se traduisent par des modifications d’indice de l’air et, donc, par des déformations de franges. Il est ainsi possible de mettre en évidence et de mesurer les particularités de l’écoulement de l’air.

3. Interférences à ondes multiples

Dans les phénomènes étudiés précédemment, on n’a considéré que les interférences produites par deux ondes provenant d’un même point de la source et présentant une certaine différence de marche. On n’a pas tenu compte des ondes multiples qui se produisent, négligeables en général par suite du faible pouvoir réflecteur de la lame. Si l’on donne à la lame un pouvoir réflecteur élevé, on ne peut plus négliger ces ondes multiples, et nous allons étudier maintenant les phénomènes qu’elles produisent. Quelques définitions sont d’abord nécessaires.

On appelle facteur de réflexion ou pouvoir réflecteur d’une surface le rapport R de l’énergie réfléchie à l’énergie incidente; il est toujours inférieur à 1. De même on appelle facteur de transmission le rapport T de l’énergie transmise à l’énergie incidente.

Lorsque les milieux sont transparents, toute l’énergie incidente se retrouve dans l’énergie réfléchie et l’énergie transmise. La conservation de l’énergie permet d’écrire:

Dans le cas de la réflexion métallique, une partie D de l’énergie est perdue par absorption. On a: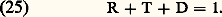

Lame à faces parallèles. Franges par transmission

Considérons deux surfaces semi-réfléchissantes parallèles AB et A B identiques (fig. 12). Un rayon incident SI¹ donne naissance à toute une série de rayons réfléchis J¹I², I²J², J²I³, etc., et il sort du système formé par AB et A B un faisceau de rayons parallèles (1), (2), (3), etc., qui peuvent interférer à l’infini. On observe donc les phénomènes dans le plan focal F d’une lentille O comme dans le cas des franges à l’infini à deux ondes. Posons:

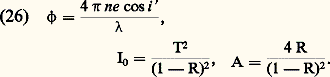L’intensité au point M du plan focal est donnée par la formule d’Airy:

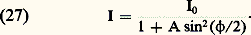Il y aura un anneau brillant au point M si sin² ( 﨏/2) = 0, c’est-à-dire si 﨏 = 2 K 神. La figure 13 montre les variations de I en fonction de 﨏. Les courbes 1, 2, 3 ont été construites pour des valeurs croissantes de R. Si R est très élevé, les franges apparaissent sous la forme d’anneaux brillants très fins se détachant sur un fond presque noir. Si K est le nombre des anneaux que l’on voit entre F et M (fig. 13), on a:

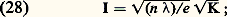cette formule donne, par exemple, le rayon angulaire i du K-ième anneau brillant, si l’on a un minimum de lumière en F.

Interféromètre de Fabry-Pérot

L’interféromètre de Fabry-Pérot se compose de deux lames épaisses en verre dont la distance est réglable. Les faces en regard AB et A B (fig. 14) ont un fort pouvoir réflecteur. On donne une forme légèrement prismatique aux deux lames de façon que les anneaux créés par les deux autres faces soient rejetés hors du champ. On observe alors, au moyen d’une lunette V visant à l’infini, les anneaux à l’infini produits par la lame d’air comprise entre AB et A B . Si l’on dispose d’une source S de petites dimensions, il est commode de projeter son image S près de la pupille d’entrée de la lunette au moyen d’un objectif O. L’interféromètre est placé devant l’objectif de la lunette.

Filtres interférentiels

Éclairons un interféromètre de Fabry-Pérot en faisceau parallèle. Utilisons une source de lumière blanche et analysons au spectroscope le faisceau émergent. D’après la relation (27), pour les longueurs d’onde correspondant à sin² ( 﨏/2) = 0, l’intensité est maximale; en dehors des valeurs de ainsi définies, la lumière n’est pratiquement pas transmise. On observe donc un spectre cannelé formé de fines cannelures brillantes se détachant sur un fond presque noir. Les cannelures sont d’autant plus étroites que les faces de l’étalon interférentiel de Fabry-Pérot ont un pouvoir réflecteur plus élevé. En donnant à l’étalon une épaisseur convenable, on peut ne laisser passer qu’une seule cannelure brillante dans le spectre visible: c’est le principe des filtres interférentiels par transmission; mais la lame d’air est remplacée par une lame mince d’un produit transparent.

Couches minces

Lorsqu’un faisceau de lumière traverse un instrument d’optique, une partie se réfléchit sur les surfaces des lentilles et retourne dans la direction de la source; on peut la considérer comme perdue pour la formation de l’image. Une fraction de cette lumière peut se réfléchir à nouveau et revenir vers l’image en formant un halo parasite. On a donc intérêt à réduire le plus possible la lumière réfléchie par les surfaces des éléments optiques d’un instrument.

Soit L une surface de verre d’indice N à traiter (fig. 15). Déposons sur elle une couche mince transparente d’épaisseur e et d’indice n . Prenons pour unité d’amplitude l’amplitude du rayon incident SI. Les amplitudes réfléchies par la couche mince sont données par les formules de Fresnel:

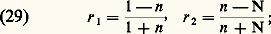la différence de phase 﨏 entre les deux rayons réfléchis, en supposant n 麗 N, s’exprime par:

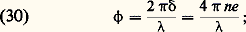l’intensité réfléchie s’écrit:

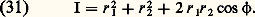Pour la longueur d’onde, il y aura minimum de lumière réfléchie si:

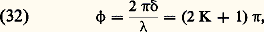d’où: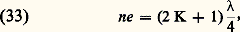

et l’intensité devient:

Il est intéressant d’utiliser l’épaisseur de couche la plus faible possible afin que la variation des phénomènes avec soit la plus petite possible. Sans la couche mince, le facteur de réflexion R du verre N seul serait:

Après traitement, c’est-à-dire dépôt de la couche n , le facteur de réflexion devient, d’après (29) et (34):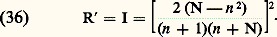

Le facteur de réflexion est peu diminué pour les indices faibles, mais la diminution est importante pour les indices forts (cf. tableau). Pour avoir extinction complète de la réflexion en lumière monochromatique de longueur d’onde, on doit d’abord réaliser la condition r ¹ = r ². D’après (29), il faut pour cela: n = N. Pour le verre optique dont les indices s’échelonnent entre 1,5 et 1,8, la racine carrée varie entre 1,22 et 1,34. Comme il n’existe pas, pour réaliser les couches, de substances utilisables d’indice inférieur à 1,34, la condition r ¹ = r ² ne peut pas être réalisée rigoureusement.

Lorsqu’on observe en lumière blanche une lame de verre traitée pour la longueur d’onde, cette radiation est presque absente dans la lumière réfléchie, dont la composition spectrale est modifiée. Comme on ne peut réaliser la diminution de la réflexion également pour toutes les longueurs d’onde du spectre, on a avantage à choisir comme longueur d’onde du minimum celle pour laquelle le récepteur a le maximum de sensibilité. Par exemple, pour l’œil, sera la longueur d’onde du jaune moyen et, par réflexion, la lame apparaîtra pourpre. Il est possible d’employer plusieurs couches superposées pour réduire encore les pertes par réflexion.

Les matériaux utilisés en infrarouge ont souvent un très haut indice de réfraction, et les pertes par réflexion deviennent alors considérables. Par exemple, le germanium, qui est transparent dans l’infrarouge, a un indice N = 4 pour = 2 猪m, et R = 0,36. Le facteur de transmission d’une lame de germanium à faces parallèles n’est donc que 0,41. Si l’on dépose sur le germanium une couche de SiO (n = 1,9) d’épaisseur optique/4, la transmission passe de 0,41 à plus de 0,90.

4. Interférométrie par granularité («speckle»)

La granularité

Faisons traverser un verre dépoli par une onde lumineuse cohérente (ou réfléchissons-la par une surface rugueuse). Chaque point du verre dépoli se comporte, d’après le principe de Huygens-Fresnel, comme une source secondaire de lumière. Les vibrations issues de ces sources peuvent interférer, mais la traversée du dépoli leur a communiqué des différences de marche variant au hasard. La figure d’interférence observée est elle aussi aléatoire. Elle est constituée de points lumineux sur fond sombre car la probabilité d’une interférence constructive est assez faible. Cette structure particulière porte le nom de granularité , ou bien celui de «speckle», d’origine anglo-saxonne (fig. 16 a).

Il est possible d’enregistrer la granularité sur une plaque photographique à grain fin. Après traitement, celle-ci se comporte comme un verre dépoli. Il est ainsi possible d’engendrer des figures de granularité rigoureusement identiques, ce qui est souvent commode.

Expérience de Burch et Tokarski

C’est l’expérience fondamentale de l’interférométrie par granularité, dont dérivent toutes les applications. À l’aide d’un faisceau laser et d’un diffuseur, formons une figure de granularité sur une plaque photographique. Après enregistrement et sans rien changer d’autre au montage, déplaçons latéralement la plaque d’une distance d de l’ordre d’une fraction de millimètre, puis enregistrons à nouveau la granularité. Après traitement, la plaque montre une double granularité dont les grains homologues sont distants de d (fig. 16 b).

Éclairons cette plaque par un faisceau de lumière parallèle. À l’infini ou, ce qui revient au même, dans le plan focal image d’un objectif nous observons des franges d’interférences à deux ondes. Comment interpréter ces franges? Chaque paire de grains se comporte comme deux trous de Young et donne naissance à des franges. Les couples de grains étant similaires, les franges sont identiques, et se superposent exactement. En outre, les paires étant réparties aléatoirement dans le plan de la plaque, tout se passe comme si les ondes qu’ils émettent étaient incohérentes; les divers systèmes de franges se superposent en intensité.

Il résulte des relations (10) et (11) que l’interfrange est donné par i =f /d où est la longueur d’onde de la lumière utilisée, f la distance focale de l’objectif et d le déplacement de la plaque photographique. Par ailleurs, ces relations supposent que les deux grains d’une paire sont identiques; s’il n’en est pas ainsi, les franges existent toujours mais leur contraste est réduit. Les deux granularités sont dites décorrélées. Bien entendu, il est possible de remplacer le déplacement de la plaque photographique par l’action d’un système optique convenable dédoublant chacun des grains, sans modifier les résultats précédents.

L’interférométrie par granularité a donc pour objet l’obtention de franges d’interférences dont l’orientation, le pas et le contraste fourniront des informations sur la modification de granularité qui leur a donné naissance. Quelques exemples vont nous permettre d’illustrer cette méthode.

Mesure de déplacements et de déformations

L’application la plus immédiate de l’expérience de Burch et Tokarski est la mesure des déplacements: l’orientation et le pas des franges fournissent immédiatement la direction et l’amplitude du déplacement de la plaque photographique. Les résultats précédents restent valables si l’on forme la figure de granularité sur un objet que l’on photographie ensuite. Une double exposition permet de mesurer le déplacement ou la déformation subis par l’objet entre les deux poses. Cette méthode est très sensible, évite tout contact avec l’objet et permet éventuellement une analyse point par point. Elle commence à être utilisée dans l’industrie du bâtiment, où elle permet de déterminer les déformations subies par des murs ou des poutres.

Mesures astronomiques

Du fait des fluctuations locales de température et de pression, l’atmosphère terrestre se comporte comme un diffuseur aléatoire rapidement variable. La lumière issue d’une étoile donne, dans le plan focal d’un télescope, une figure de granularité de diamètre global voisin de 1 d’arc, et dont chaque grain a la taille de la figure de diffraction de l’objectif du télescope. Une pose courte, de l’ordre de 10^-2 s, permet d’enregistrer cette granularité, alors qu’une pose plus longue provoque un brouillage, les grains se déplaçant rapidement.

Deux étoiles voisines, comme les composantes d’une étoile double, donnent une double granularité, comme dans l’expérience de Burch et Tokarski. L’enregistrement éclairé par un faisceau de lumière parallèle montre des franges d’interférence dont l’orientation et le pas permettent de déterminer l’orientation et la distance angulaire des étoiles, avec une précision très supérieure à celle que fournit l’observation directe. Il est bon de noter que deux clichés de la même étoile donnent les mêmes franges d’interférences, puisque celles-ci sont indépendantes des positions des couples de grains. Il est alors possible d’enregistrer un grand nombre de clichés puis de superposer les systèmes de franges associés, ce qui améliore beaucoup la qualité des mesures.

Des variantes de cette méthode, due à l’astronome français Antoine Labeyrie, permettent d’obtenir d’autres informations, comme le diamètre apparent d’étoiles ou la répartition de température à leur surface. La sensibilité est telle qu’il est possible – théoriquement du moins – de mettre en évidence l’existence de planètes autour d’une étoile.

Mesure de rugosité

La granularité – soit la figure d’interférence obtenue – résulte de la diffusion de la lumière par les irrégularités du diffuseur. Il existe donc une relation entre cette figure et les irrégularités du diffuseur. En fait, dans la plupart des applications, il est possible d’ignorer cette relation. Toutefois, une variante de l’expérience de Burch et Tokarski, encore largement empirique, permet de déterminer la valeur moyenne des irrégularités, la rugosité, à partir du contraste des franges. Plusieurs activités font appel à cette méthode, par exemple le traitement électrolytique des surfaces.

Traitement d’images

Une autre application est le traitement d’images que nous illustrons par la recherche de la différence. Le problème posé est le suivant: soit deux photographies ne différant que par de petits détails, difficiles à distinguer par observation directe. Est-il possible d’isoler ces détails en supprimant des photographies les parties communes? Une solution est fournie par l’utilisation des figures de granularité. Sur une même plaque photographique, nous enregistrons les deux images, en les décalant légèrement, après avoir superposé à chacune d’elles la même figure de granularité. Aux parties communes sont ainsi associées des paires de grains identiques et aux détails différents, des couples de grains dissemblables. L’interférence est totalement destructrice pour les premiers, alors qu’elle ne l’est que partiellement pour les autres. Autrement dit, il existe des endroits du plan d’observation où les parties communes n’envoient pas de lumière, les franges sombres. En ces endroits, il subsiste de la lumière en provenance des détails différents. Une fente convenablement placée permet d’isoler cette lumière et, par suite, d’éliminer les parties communes aux deux images.

5. Applications des interférences

On n’examinera ici ni la spectroscopie interférentielle, traitée dans l’article SPECTROSCOPIE, ni les applications de l’holographie à l’interférométrie (cf. OPTIQUE – Optique cohérente).

Microscopes interférentiels

Les objets transparents sont nombreux en biologie, et les microscopistes sont obligés d’avoir recours à des méthodes de coloration pour les apercevoir. Dans le cas d’objets vivants, leurs effets sont très nuisibles et l’intérêt des microscopes interférentiels est de permettre l’observation d’objets vivants dans des conditions de contraste aussi favorables que dans l’étude des objets morts après coloration. Un autre avantage de ces instruments est qu’il est possible de mesurer l’indice ou l’épaisseur des éléments transparents examinés. Enfin leur emploi ne se limite pas à la biologie, et ils trouvent de nombreuses autres applications en chimie, en physique et dans différentes techniques industrielles.

Le principe des microscopes interférentiels à deux ondes est le même que celui des interféromètres ordinaires. Un rayon lumineux SM, issu du condenseur (fig. 17), donne naissance en M à deux rayons, sous l’effet de l’un des éléments de l’interféromètre: le rayon MAN traverse l’objet déphasant A, tandis que le rayon MBN passe à côté; sous l’action d’un autre élément de l’interféromètre, ces deux rayons se rejoignent en N pour former un rayon unique qui pénètre alors dans le microscope. Le phénomène est le même pour tous les rayons issus du condenseur. On a donc une onde incidente plane ⁰ qui est dédoublée à partir de M en deux ondes ¹ et ². L’onde ² est déformée à la traversée de l’objet A, alors que l’onde ¹ n’est pas modifiée. La distance des deux ondes, c’est-à-dire leur différence de marche, est réglée au moyen de l’interféromètre.

Si = 0, les deux ondes sont en phase dans les régions autres que celle déformée par l’objet A, et l’intensité lumineuse a, par exemple, la valeur I⁰. Si l’objet A introduit une différence de marche 嗀, on observe dans l’image de A une intensité;

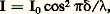différente de I⁰, et l’objet transparent devient visible. Dans le cas où 嗀 =/2, l’objet apparaît en noir sur fond blanc. D’une façon générale, si est différent de zéro, on aura une intensité:

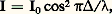en dehors de l’objet et une intensité:

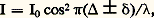dans l’image de l’objet. Si et 嗀 sont petits, on observera en lumière blanche les teintes interférentielles de l’échelle de Newton: l’image de l’objet apparaîtra avec une teinte différente de celle du reste du champ.

La figure 18 donne le principe du microscope interférentiel de Leitz. La lumière provenant de la source S est séparée en deux faisceaux (1) et (2) par la lame semi-réfléchissante L¹. Le faisceau (1) traverse L¹, se réfléchit sur le miroir M¹, traverse l’objet P, l’objectif ¹ du microscope, puis se réfléchit sur la lame semi-réfléchissante L² et pénètre dans l’oculaire ². Le faisceau (2) est réfléchi par la lame L¹, le miroir M², traverse une préparation R de référence, un objectif O ¹, la lame L² et pénètre dans l’oculaire ². Les interférences entre (1) et (2) permettent d’observer les détails déphasants de la préparation.

On peut aussi observer, avec des microscopes interférentiels spéciaux, les objets réfléchissants. L’emploi des interférences à ondes multiples donne une excellente précision, spécialement dans l’étude des états de surface.

Mesure du mètre en longueurs d’onde

On peut appliquer les méthodes interférentielles à la mesure du mètre international. On détermine combien de longueurs d’onde d’une radiation déterminée sont contenues dans la longueur de l’étalon déposé au Bureau international des poids et mesures (cf. MESURE – Étalons fondamentaux).

Dans les premières mesures effectuées par A. Michelson (1892) puis par R. Benoît, C. Fabry et A. Pérot (1913), la radiation utilisée était la raie rouge du cadmium, radiation la plus monochromatique connue à l’époque. Elle n’était cependant pas suffisamment monochromatique pour permettre d’atteindre des différences de marche de l’ordre du mètre et comparer directement le mètre étalon à une longueur d’onde. Il a donc fallu procéder par étapes successives avec d’assez grandes difficultés.

Grâce aux progrès réalisés dans la construction des sources, les mesures directes sont devenues possibles. Pour obtenir une raie très fine, il faut employer un gaz sous faible pression à basse température et se servir d’un corps ayant un poids atomique élevé. Ernst Engelhard a mis au point une source qui répond bien à ces conditions: elle émet la radiation orangée du krypton 86 dont la longueur d’onde est 0,605 6 猪m. Les petites variations de longueur d’onde de cette raie en fonction des conditions de fonctionnement de la lampe ont été mesurées indépendamment par E. Engelhard au Physikalische-Technische Bundesanstalt et par J. Terrien au Bureau international des poids et mesures. Une extrapolation des résultats à la pression nulle a permis de connaître la longueur d’onde pour des atomes immobiles et non perturbés. Cette longueur d’onde est un étalon naturel de longueur cinquante fois plus précis que le prototype en platine iridié. Le Comité international des poids et mesures a décidé que le mètre serait défini comme la longueur égale à 1 650 763,73 fois la longueur d’onde dans le vide de la radiation correspondant à la transition entre les niveaux 2p ¹⁰ et 5d ⁵ de l’atome de krypton 86.

Encyclopédie Universelle. 2012.